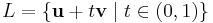Line segment

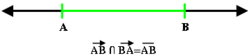
The geometric definition of a line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment is either an edge (of that polygon) if they are adjacent vertices, or otherwise a diagonal. When the end points both lie on a curve such as a circle, a line segment is called a chord (of that curve).

1 Definition
2 Properties
3 In proofs
4 See also
5 References
6 External links

Definition

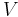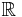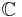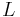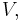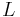If $V\,\!$ is a vector space over $\mathbb{R}$ or $\mathbb{C}$ , and $L\,\!$ is a subset of $V,\,\!$ then $L\,\!$ is a line segment if 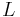$L\,\!$ can be parameterized as

$L = \{ \mathbf{u}+t\mathbf{v} \mid t\in[0,1]\}$

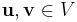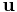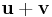for some vectors $\mathbf{u}, \mathbf{v} \in V\,\!$ , in which case the vectors $\mathbf{u}$ and $\mathbf{u+v}$ are called the end points of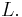 $L.\,\!$

Sometimes one needs to distinguish between "open" and "closed" line segments. Then one defines a closed line segment as above, and an open line segment as a subset 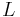$L\,\!$ that can be parametrized as

$L = \{ \mathbf{u}+t\mathbf{v} \mid t\in(0,1)\}$

for some vectors 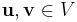$\mathbf{u}, \mathbf{v} \in V\,\!$ .

An alternative, equivalent, definition is as follows: A (closed) line segment is a convex hull of two points.

Properties

A line segment is a connected, non-empty set.
If 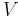$V$ is a topological vector space, then a closed line segment is a closed set in 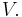$V.$ However, an open line segment is an open set in 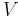$V$ if and only if 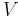$V$ is one-dimensional.
More generally than above, the concept of a line segment can be defined in an ordered geometry.

In proofs

In geometry, it is sometimes defined that a point B is between two other points A and C, if the distance AB added to the distance BC is equal to the distance AC.

In an axiomatic treatment of Geometry, the notion of betweenness is either assumed to satisfy a certain number of axioms, or else defined in terms of an isometry of a line (used as a coordinate system).

Segments play an important role in other theories. For example, a set is convex if the segment that joins any two points of the set is contained in the set. This is important because it transforms some of the analysis of convex sets to the analysis of a line segment.

References

David Hilbert: The Foundations of Geometry. The Open Court Publishing Company 1950, p. 4

External links

Line Segment at PlanetMath
Definition of line segment With interactive animation
Copying a line segment with compass and straightedge
Dividing a line segment into N equal parts with compass and straightedge Animated demonstration

This article incorporates material from Line segment on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.